D sin фи k лямбда формула обозначения

Обновлено: 29.01.2025

Дифракционная решетка – это простейший спектральный прибор, состоящий из системы щелей (прозрачных для света участков), и непрозрачных промежутков, которые сравнимы с длиной волны.

Одномерная дифракционная решетка, состоит из параллельных щелей одинаковой ширины, которые лежат в одной плоскости, разделяемых одинаковыми по ширине непрозрачными для света промежутками. Лучшими считаются отражательные дифракционные решетки. Они состоят из совокупности участков, отражающих свет и участков, которые свет рассеивают. Данные решетки представляют собой отшлифованные металлические пластины, на которые рассеивающие свет штрихи нанесены резцом.

Картиной дифракции на решетке — является результат взаимной интерференции волн, идущих ото всех щелей. С помощью дифракционной решетки реализуется многолучевая интерференция когерентных пучков света, подвергшихся дифракции и которые идут от всех щелей.

Характеристикой дифракционной решетки служит ее период. Периодом дифракционной решетки (d) (ее постоянной) называют величину, равную:

где a — ширина щели; b — ширина непрозрачного участка.

Дифракция на одномерной дифракционной решетке

Допустим, что перпендикулярно к плоскости дифракционной решетки падает световая волна с длиной . Так как щели у решетки расположены на равных расстояниях друг от друга, то разности хода лучей ( ), идущих от двух соседних щелей, для направления будут одинаковы для всей рассматриваемой дифракционной решетки:

Главные минимумы интенсивности наблюдаются в направлениях, определенных условием:

$a\sin \varphi =\pm k\lambda \ (k=1,2,3\dots )} \qquad (3)$

Кроме главных минимумов, в результате взаимной интерференции лучей света, которые идут от двух щелей, в некоторых направлениях лучи гасят друг друга. В результате возникают дополнительные минимумы интенсивности. Они появляются в тех направлениях, где разность хода лучей составляют нечетное число полуволн. Условием дополнительных минимумов является формула:

$d{\sin \varphi =\pm k'\frac{\lambda}{N}\qquad \left(k'=1,2,\dots ,N-1,N+1,\dots ,2N-1,2N+1,\dots \right)} \qquad (4)$

где N – количество щелей дифракционной решетки; — целые значения кроме 0, В том случае, если решетка имеет N щелей, то между двумя главными максимумами находятся дополнительный минимум, которые разделяют вторичные максимумы.

Условием главных максимумов для дифракционной решетки является:

$d{\sin \varphi =\pm m\lambda (m=0,1,2,\dots )} \qquad (5)$

Величина синуса не может быть больше единицы, то количество главных максимумов:

$d{\sin \varphi =m\lambda (m=0,1,2,\dots )} \qquad (1.1)$

По условию задачи Так как угол отклонения лучей можно считать малым ( ), то примем, что:

Из рис.1 следует, что:

$tg\ \varphi =\frac{l}{2}:L=\frac{l}{2L} \qquad(1.3)$

Подставим в формулу (1.1) выражение (1.3) и учтем, что , получим:

Из (1.4) выразим период решетки:

Задание	Используя условия примера 1, и результат решения, найдите количество максимумов, которое даст рассматриваемая решетка.
Решение	Для того чтобы определить максимальный угол отклонения лучей света в нашей задаче найдем число максимумов, которое может дать наша дифракционная решетка. Для этого используем формулу:

$d{\sin \varphi =m\lambda \left(m=0,1,2,\dots \right)} \qquad (2.1)$

где положим, что при . Тогда, получим:

Следует учесть при вычислениях, что число обязательно целое и синус угла обязательно меньше единицы. При этом общее количество максимумов картины дифракции справа и слава от центрального максимума одинаково и равно:

${m'}_{max}=2m_{max}=2\frac{d}{\lambda }\ \qquad(2.3)$

Необходимо учесть центральный максимум, поэтому суммарное число максимумов равно:

Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных щелей, равноудаленных друг от друга.

Суммарная ширина щели и штриха (a+b=d) – период решетки.

! d=((a+b)*N)/N=C/N!, где С –ширина решетки, N -число штрихов на ней.

на нем: Л- линза; Р – решетка; Э - экран

Максимумы, которые образуются на экране, после интерференции вторичных волн, идущих от узких щелей, удовлетворяют условию:

!d*sin фи = k*лямбда! - формула дифракционной решетки.

фи - угол дифракции (угол отклонения от прямолинейного направления);

k - порядок спектра;

лямбда - длина волны света, освещающего решетку,

Дифракционные спектры для монохроматического света представляет собой чередование максимумов и минимумов по обе стороны от центрального механизма. Максимумы имеют цвет соответствующей длины света, освещающего решетку.

Если решетку освещать белым светом, то центральный максимум будет белым, а остальные будут представлять собой чередование цветных полос плавно переходящих друг в друга, т. к. sin фи= k*лямбда/d - зависит от длины волны света. D = к/t - угловая дисперсия решетки. R =k*N - разрешающая способность.

Диффузия в жидкости. Уравнение Фика. Уравнение диффузии для мембран.

Диффузия - самопроизвольное проникновение молекул одного вещества между молекулами других.

Явление диффузии - важный элемент диффракционирования мембран. При диффузии происходит перенос массы вещества. В биофизике это называется транспорт частиц. Основным уравнением диффузии является уравнение Фика:

где I – плотность частиц при диффузии в жидкость.

D – коэффициент диффузии.

Коэффициент 1/3 возник ввиду трехмерного пространства и хаоса в движении молекул (в среднем в каждом из 3-х направлений перемещается 1/3 часть всех молекул)

сигма - средняя длина свободного пробега молекул

тау -среднее время оседлой жизни молекул

С- массовая концентрация молекул

Х- перемещение молекул вдоль оси X

- градиент массовой концентрации

Уравнение диффузии можно записать в виде:

n – концентрация молекул.

Градиент концентрации

R- универсальная газовая постоянная; Т- абсолютная температура градиент химического потенциала,

Тогда

С - концентрация частиц. А Эйнштейн показал, что D пропорционально Т. Дня биологических мембран уравнение Фика имеет вид:

- концентрация молекул внутри клеток

- коэффициент проницаемости

l – толщина мембраны.

Дифракция света на щелях.

Дифракцией света называют явление отклонения света от прямолинейного распространения в среде с резкими неоднородностями.
Описать картину дифракции можно с учетом интерференции вторичных волн.

Рассмотрим дифракцию от узкой щели (АВ)

MN – непрозрачная преграда;

АВ=а – ширина щели;

АВ – часть волновой поверхности, каждая точка которой является источником вторичных волн, которые распространяются за щелью по разным направлениям. Линза соберет лучи А, А₁ и В в точке О₁ экрана.

АD - перпендикуляр к направлению пучка вторичных волн. Разбили ВD на отрезки =лямда/2.

АА₁, А₁В - зоны Френеля. Вторичные волны, идущие от двух соседних зон Френеля, не гасят друг друга, так как отличаются по фазе на пи. Число зон, укладывающихся в щели, зависит от длины волны лямда и угла альфа.

Если щель АВ разбить при построении на нечетное число зон Френеля, а ВD на нечетное число отрезков, равных лямда/2, то в точке О₁ наблюдается максимум интенсивности света. ВD=а*sinα=+-(2k+1)*лямда/2.

Если щель разбить на четное число зон Френеля, то наблюдается минимум освещенности: а*sinα=+-2k*лямда/2=+-k*лямда.

Поэтому на экране получится система светлых (mах) и темных (min) полос симметричных относительно центра (альфа=треугольник - изменение) - наиболее яркой полосы.

Интенсивность остальных максимумов убывает с увеличением к.

3аконы излучения абсолютно чёрного тела (Стефана - Больцмана, Вина). Формула Планка. Использование термографии в диагностике.

Излучение чёрного тела имеет сплошной спектр. Графически это выглядит для разных температур так:

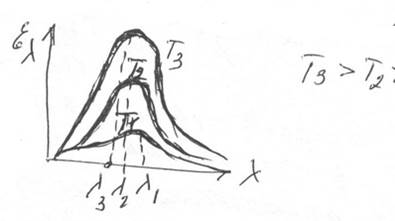
Существует максимум спектральной светимости, который при повышении

температуры смещается в сторону коротких волн.

По мере нагревания чёрного тела его энергетическая светимость (Re)

увеличивается: Re = опред интеграл от 0 до бескон от Eлямда*dлямда

Стефан и Больцман установили, что Re=сигма*T^4

Сигма = 5,6696*10^-8 Вт/K*м^2 - постоянная Стефана-Больцмана,

T=t+273 - абсолютная (термодинамическая) температура по шкале

Кельвина. Все замечали это на практике, чем выше температура спирали, нагретой печи, тем больше они излучают тепла.

Планк получил формулу для спектральной плотности абсолютно черного тела (Eлямда) и серого тела (r лямда) (лямда-индекс): Eлямда=2п*h*c^2/лямда^5 * 1/exp[h*c/k*T*лямда-1]

альфа - коэффициент поглощения

h - постоянная Планка;

С - скорость света в вакууме;

лямда - длина волны;

k - постоянная Больцмана;

Т - абсолютная температура.

2 Затухающие колебания и декремент затухания. Апериодические колебания.

Свободные колебания (происходящие без внешнего воздействия периодически действующей силы) являются затухающими. График затухающих колебаний имеет вид:

Амплитуда колебаний с каждым разом убывает. Затуханию способствуют силы трения и сопротивления, возникающие в средах. Пусть r-коэффициент трения, характеризующий свойство среды оказывать сопротивление движению. Тогда БЕТТА= r/2m – коэффицент затухания.

Wo= корень(K/m) – циклическая частота собственных колебаний, тогда W^2=Wo^2-БЕТТА^2, где W – циклическая частота затухания колебаний.

Быстрота затухания колебаний определяется коэффициентом затухания. Уравнение затухающих колебаний имеет вид А=Ао*l в степени минус бета*t

Ao – первоначальная амплитуда, А-амплитуда затухающих через время t.

Лямда=lnA(t)/A(t+T)=lnAo*(e в степени минус бета*t)/Ao*e^-бета*(t+T)=ln(e^ бета*t) –логарифмический декрет затухания.

!Лямда=бета*Т!- связь логарифмического декремента затухания с коэффициентом затухания. При сильно затухании колебания становятся апериодическими (если бета^2>Wo^2)

№31 Импеданс полной цепи переменного тока. Сдвиг фаз. Резонанс напряжения.

Рассмотрим последовательно соединенные R, L, C.

При последовательном соединении:

1) Uвх=U0*cosW*t=Ur+Ul+Uc – входное напряжение.

2) I=I0*cos(W*t-фи) – сила тока в цепи.

Начертим векторную диаграмму:

Ur0 – совпадает по фазе с силой тока;

Ul0 – опережает на пи/2;

Uc0 – отстает от тока на пи/2.

По теореме Пифагора: (U0)^2=(U0r)^2+(U0l-U0c)^2

Сократив обе части уравнения на (I0)^2 получим выражение для полного сопротивления (Z):

Z=квадратный корень из (R^2+(W*L-1/W*c)^2) – импеданс.

Если сопротивление катушки Xl= W*L равно сопротивлению конденсатора Xc=1/W*c, то полное сопротивление Z=R; по закону Ома Iрез=U0/Z=U0/R (Iрез – резонансный ток) – сила тока резко возрастает – РЕЗОНАНС. При этом Ul=Uc>>U0 – резонанс напряжений. Это возможно, т.к. Ul и Uc сдвинуты по фазе между собой на пи:

При этом на резисторе R выделяется максимальное количество теплоты:

№32 Импенданс тканей организма. Эквивалентная Электрическая схема. Оценка жизнеспособности тканей и органов но частотной зависимости к углу сдвига фаз.

Ткани организма проводят как постоянный так и переменный ток. Биологическая мембрана а значит и весь организм обладает емкостным сопротивлением, т.к. обладают емкостью, т.е. способны

накапливать заряд. При пропускании через живые ткани переменного тока наблюдается отставание напряжения от тока. Омические емкостные свойства биологических тканей можно моделировать используя эквивалентные электрические схемы, при любых частотах зависимость сдвига фаз и импенданса от частоты выполняется для схемы

1/Zв2=1/Rв2+1/корень(R1 в2+1/Wв2*Св2)!, где Z-полное сопротивление данной цепи, с - ёмкость.

При малых частотах: Z=R2 При больших частотах: Zmin=(R1*R2)/(R1+R2).

Графическое изображение зависимости импенданса живой ткани от частоты переменного тока.

Сдвиг фаз между током и напряжением tg фи = R/Xc=RWC (1).

Частотная зависимость сдвига фаз живой ткани. При отмирании ткани натрий-калиевый канал биологических мембран разрушается, цитоплазма

клетки (проводник) соединяется с межклеточной

жидкостью(проводник) и емкостные свойства ткани уменьшаются, а это значит, что и импенданс (Z) и сдвиг фаз (фи) меньше зависят от частоты. Мёртвая ткань обладает лишь омическим сопротивлением (R), и не зависит от частоты. Диагностический метод, основанный на регистрации изменения импенданса тканей и сдвига фаз называется РЕОГРАФИЕЙ.

Поскольку в условии сказано, что линза фокусирует свет на экран, а после прохождения дифракционной решетки на нее по-прежнему падают параллельные пучки света (правда направленные под разными углами к главной оптической оси), значит, что на экране располагается фокальная плоскость линзы? ее фокус равен F = 1,8 м. Дифракционные максимумы наблюдаются под углами (эти углы отсчитываются как раз от оптической оси линзы), определяемыми соотношением d синус альфа =k\lambda , где k — номер максимума. После прохождения решетки все лучи, относящиеся к определенному максимуму параллельны друг другу. Линза преломляет все лучи, кроме луча, прошедшего через ее оптический центр. Пересечение этого луча с плоскостью экрана и определяет положение дифракционного максимума на экране. Нулевой максимум располагается прямо за оптическим центром. Определим номер максимума, отстоящего от этой точки на h = 21см. Из рисунка ясно, что tg альфа = дробь, числитель — h, знаменатель — F В условии задачи сказано, что углы можно считать малыми, а значит, для номера максимума имеем: k= дробь, числитель — d синус альфа , знаменатель — \lambda \approx дробь, числитель — dtg альфа , знаменатель — \lambda = дробь, числитель — dh, знаменатель — \lambda F = дробь, числитель — 10 в степени минус 5 умножить на 0,21, знаменатель — 580 умножить на 10 в степени минус 9 умножить на 1,8\approx 2

Новые вопросы в Физика

Определите толщину диэлектрика конденсатора, электроёмкость которого , площадь покрывающих друг друга пластин , если диэлектрик - слюда

Груз падает без начальной скорости. Определите скорость движения груза через 5 с после начала падение. можно решение

Известно, что в солёной воде скорость распространения света в 1,45 раз(-а) меньше, чем в вакууме. Чему равна глубина залива, если за 7,7-10-8 с нормал … ьно падающий луч успевает достигнуть дна, отразиться и вернуться назад. Ответ (округли до десятых)м

Чи вірне твердження? На вершині Говерли повітря розріджене, отже, тиск менший. Це значить, що температура кипіння води менша за 100 °C.

1Вкажіть як зміниться сила Архімеда, яка діє на тіло, повністю занурене у рідину, якщо густина рідини зменшилась у 1,3 рази варіанти відповідей 1не зм … іниться .2.зменшиться у 2,6 разів.3.збільшиться у 1,3 рази.4.зменшиться у 1,3 рази

Лабораторная работа «Условия плавания тел в жидкости (домашняя исследовательская работа) Тема: Выяснение условий плавания тела в жидкости Цель работы: … Выяснить условия плавания тела в жидкости. Оборудование: Широкий сосуд с водой, нитки, таблица плотностей, однородные физические тела из различных веществ (лед, дерево, пластмасса, сталь, фарфор, пробка, мыло, резина), неоднородные (например, пузырек с песком или с воздухом, губка, резиновый мячик и т.д.), таблица плотностей. Внимание, соблюдайте технику безопасности! 1. Изучите инструкцию, подготовьте оборудование. 2. Будьте внимательны. Не торопитесь. 3. Используйте воду комнатной температуры. 4. Сосуд с водой на край стола не ставьте (если он стеклянный, то может упасть и разбиться). 5. Если опыты проводите в ванне, то не сливайте воду, пока не достанете все предметы, а также не используйте слишком мелкие предметы. 6. В опытах с другой жидкостью, воду НЕ ПОДКРАШИВАТЬ, чтобы не произошла опасная химическая реакция с другим веществом. Указания к работе Часть I 1. По таблице в учебнике на странице 61-63 определите плотность воды – вещества, в которое вы будете погружать физические тела. 2. Начертите таблицу в тетрадь и в ходе наблюдений заполняйте ее, либо заполняйте таблицу в данном файле. 3. Сначала проводите исследование с однородными простыми физическими телами, плотность которых всюду одинакова (например, ложка алюминиевая). Поведите минимум три опыта. 4. По очереди погружайте в сосуд с водой различные физические тела, записывайте в таблицу свои наблюдения (всплывает, плавает внутри жидкости, тонет). 5. По таблице в учебнике на странице 61-63 для каждого физического тела определите плотность вещества, запишите ее в таблицу и сравните с плотностью воды (больше, меньше или равно). 6. Посмотрите в таблицу. 7. Какие физические тела всплывают, из каких веществ они состоят? 8. Какие физические тела плавают внутри жидкости, из каких веществ они состоят? 9. Какие физические тела тонут, погружаясь на дно, из каких веществ они состоят? 10. Сделайте вывод о том какая должна быть у тела плотность по сравнению с водой, чтобы оно плавало/тонуло/всплывало. Часть II 1. Рассмотрите сложное физическое тело, с неоднородным составом, погружая его в воду. Запишите, пользуясь таблицей, плотности веществ, из которых оно состоит. 2. Наблюдая за расположением тела в воде, сделайте вывод о его средней плотности в сравнении с плотностью воды (больше, меньше, равно) и запишите в таблицу. Часть III 1. Исследуйте жидкости с разной плотностью. Жидкости НЕ ПОДКРАШИВАТЬ, чтобы не произошла опасная химическая реакция с другим веществом. 2. Выдавите с помощью пипетки или шприца растительное масло в середине сосуда, заполненного водой, и посмотрите, что произойдет с маслом (поднимется вверх, останется в середине или осядет на дно). Какую можно сделать гипотезу о соотношении плотностей воды и масла? Найдите плотность масла в таблице и проверьте свою гипотезу. 3. С помощью таблицы плотностей подберите такие жидкости (безопасные), чтобы одна жидкость, не всплывая на поверхность, оставалась в середине другой. Проведите опыт. Ход работы Плотность воды = _____________ (по таблице) № опыта Название тела и вещества Плотность вещества* (кг/м3) Состояние тела в жидкости (всплывает, плавает внутри, тонет, плавает на поверхности) Сравниваем с плотностью воды >,<,= Пример Алюминиевая ложка 2700 тонет 2700 >1000 больше 1 2 Неоднородное тело (название) 3 4 Жидкость (название) *-таблица плотностей в учебнике на стр 61-63. Вывод. Сделайте вывод о том какая должна быть у тела плотность по сравнению с водой, чтобы оно плавало / тонуло / всплывало. Контрольный вопрос: Как вы считаете, почему некоторые неоднородные предметы (например, стеклянный пузырек с песком и воздухом, кораблик пластиковый, резиновый мячик и т.д.)

Определи соответствующую команду,используемую при сохранение файла: создаётся копия ранее созданной презентации и в нее вносятся изменения,в итоге пол … учаются два файла с некоторыми различаями.это ЦГ.

Начнем с того, что узнаем, что такое дифракционная решетка.

Дифракционной решеткой – это прибор, благодаря которому осуществляется периодическая модуляция падающей волны света по фазе и амплитуде.

Амплитудная дифракционная решетка

Допустим, что у нас есть одномерная амплитудная решетка, в которой находятся затемненные промежутки и параллельные щели. Число щелей равно N , ширину щелей обозначим как b , а период решетки как d .

Если свет падает на нее нормально, то мы можем определить разность хода (дельту) монохромного света, испускаемого соседними щелями:

Фазовый сдвиг рассчитывается по формуле:

Здесь υ = sin ν λ обозначает пространственную частоту. Результирующая амплитуда будет равна сумме геометрической прогрессии:

Амплитуда поля после прохождения одной щели здесь обозначена как E 1 .

Чтобы найти интенсивность света, который проходит сквозь амплитудную дифракционную решетку, нужно воспользоваться формулой:

Параметр I 0 – интенсивность света, падающего на решетку, I 1 – интенсивность той части света, который проходит через одну щель, а I N – интенсивность с учетом многолучевой интерференции.

Интенсивность всех пучков света в этом случае будет одинаковой.

Функция I N будет иметь нулевой числитель и знаменатель, если будет выполняться условие главных максимумов.

Таким образом, если данные максимумы будут выполнены, то свет, совершающий дифракцию на решетке с N -ным количеством щелей, увеличит свою интенсивность в N 2 раз. Данная зависимость обусловлена таким явлением, как многолучевая интерференция пучков, проходящих через регулярные структуры.

Из формулы, приведенной выше, можно сделать вывод, что чем выше порядок, тем меньше интенсивность главных максимумов. Также имеется зависимость от отношения d b – целое число.

Если максимумы порядков d b , 2 d b и т.д. будут приходиться на минимумы дифракции в одних щелях, то интенсивность света снизится до нуля. Например, при d b = 2 мы будем наблюдать равенство прозрачной и непрозрачной частей, в спектре решетки при этом останутся только главные максимумы нечетных и нулевых порядков, а четных среди них не останется совсем.

Если число щелей в решетке равно N , то она будет создавать в промежутках между максимумами N - 1 минимальную освещенность и N - 2 побочных максимумов. Чем больше будет щелей, тем меньше будет относительная интенсивность дополнительных максимумов. При достижении определенного предела их существованием и вовсе можно пренебречь.

Если же свет падает на решетку наклонно, то пространственная частота будет отличаться от нуля, и условие главных максимумов станет частью разности пространственных частот. Образование пространственного спектра дифракционной решетки будет подчиняться принципам Фурье.

Дифракционная решетка имеет следующие характеристики спектральных свойств:

угловую дисперсию D : D = m d cos ν ;
разрешающую способность R : λ ∆ λ = m N ;
свободную дисперсионную область G : G = λ m (данная величина определяет диапазон спектра, свободный от перекрытия).

Сочетание свойств амплитудных дифракционных решеток делает их невыгодными для использования на практике. Они разбрасывают свет по многим порядкам, а основная часть энергии в них приходится на ахроматический нулевой порядок, и в максимумы высоких порядков в итоге попадает недостаточно света.

Фазовая дифракционная решетка

Такой тип решеток имеет гораздо лучшие спектральные свойства. Они характеризуются определенным профилем штрихов.

Фазовые дифракционные решетки бывают прозрачными и отражательными. Оба типа практически не оказывают влияния на амплитуду волны света, однако периодически влияют на ее фазу.

Условие: сформулируйте объяснение, чем именно определяется разрешающая способность дифракционной решетки.

Решение

Мы можем определить разрешающую способность данного типа решеток следующим образом:

Если у решетки много штрихов (под "много" здесь подразумевается несколько десятков тысяч), то она имеет высокую разрешающую способность. Чтобы увеличить значение данного показателя, нужно увеличить порядки интерференции ( m ) , однако их количество ограничено углами отклонения ν ≤ π 2 . Значит, sin ν в выражении d sin ν = m λ ( m = 0 , ± 1 , ± 2 , . . . ) не может превышать единицы.

Следовательно, m m a x = d λ . В итоге получаем, что:

Таким образом, чем больше N , тем лучшую угловую дисперсию будет иметь решетка.

Из приведенной выше формулы мы можем вывести, что:

d cos ν δ ν = m δ λ .

Значит, R = m d cos ν .

Данное выражение означает, что чем меньше d , тем выше угловая дисперсия. На практике большее значение будут иметь решетки значительной общей ширины и с большим N .

Условие: охарактеризуйте отличия фазовой дифракционной решетки с точки зрения картины интерференции.

Решение

Интерференционная картина для нее имеет неизменный характер. Меняться будет только распределение интенсивностей. Максимум при этом будет размещаться не в главном максимуме на угле ν = 0 , а на том максимуме, что попадет на угол ν = ( n - 1 ) α или же будет размещаться рядом с ним. Это позволит нам работать с высокими порядками интерференции, поскольку разрешающая способность решетки будет выше (без уменьшения потерь интенсивности).

Дифракционная решетка — оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга, щелей.

Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места — щели — будут пропускать свет; штрихи, соответствующие промежутку между щелями, рассеивают и не пропускают света. Сечение такой дифракционной решетки (а) и ее условное обозначение (б) показаны на рис. 19.12. Суммарную ширину щели а и промежутка б между щелями называют постоянной или периодом дифракционной решетки:

с = а + б. (19.28)

Если на решетку падает пучок когерентных волн, то вторичные волны, идущие по всевозможным направлениям, будут интерферировать, формируя дифракционную картину.

Пусть на решетку нормально падает плоскопараллельный пучок когерентных волн (рис. 19.13). Выберем некоторое направление вторичных волн под углом a относительно нормали к решетке. Лучи, идущие от крайних точек двух соседних щелей, имеют разность хода d = А'В'. Такая же разность хода будет для вторичных волн, идущих от соответственно расположенных пар точек соседних щелей. Если эта разность хода кратна целому числу длин волн, то при интерференции возникнут главные максимумы, для которых выполняется условие ÷А'В¢÷= ± kl, или

где k = 0,1,2. — порядок главных максимумов. Они расположены симметрично относительно центрального (k = 0, a = 0). Равенство (19.29) является основной формулой дифракционной решетки.

Между главными максимумами образуются минимумы (добавочные), число которых зависит от числа всех щелей решетки. Выведем условие для добавочных минимумов. Пусть разность хода вторичных волн, идущих под углом a от соответственных тoчек соседних щелей, равна l/N, т. е.

d = с sin a= l/N, (19.30)

где N — число щелей дифракционной решетки. Этой разности хода 5 [см. (19.9)] отвечает разность фаз Dj= 2p/N.

Если считать, что вторичная волна от первой щели имеет в момент сложения с другими волнами нулевую фазу, то фаза волны от второй щели равна 2p/N, от третьей — 4p/N, от четвертой — 6p/N и т. д. Результат сложения этих волн с учетом фазового различия удобно получить с помощью векторной диаграммы: сумма N одинаковых векторов напряженности электрического поля, угол (разность фаз) между любыми соседними из которых есть 2p/N, равна нулю. Это означает, что условие (19.30) соответствует минимуму. При разности хода вторичных волн от соседних щелей d = 2(l/N) илиразности фаз Dj = 2(2p/N) будет также получен минимум интерференции вторичных волн, идущих от всех щелей, и т. д.

В качестве иллюстрации на рис. 19.14 изображена векторная диаграмма, соответствующая дифракционной решетке, состоящей из шести щелей: и т. д. — векторы напряженности электрической составляющей электромагнитных волн от первой, второй и т. д. щелей. Возникающие при интерференции пять добавочных минимумов (сумма векторов равна нулю) наблюдаются при разности фаз волн, приходящих от соседних щелей, в 60° (а), 120° (б), 180° (в), 240° (г) и 300° (д).

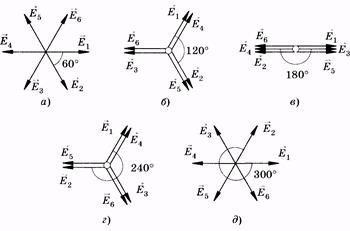
Рис. 19.14

Так, можно убедиться, что между центральным и каждым первым главным максимумами имеется N -1 добавочных минимумов, удовлетворяющих условию

Между первым и вторым главными максимумами также расположены N - 1 добавочных минимумов, удовлетворяющих условию

и т. д. Итак, между любыми двумя соседними главными максимумами наблюдается N - 1 добавочных минимумов.

При большом количестве щелей отдельные добавочные минимумы практически не различаются, а все пространство между главными максимумами выглядит темным. Чем больше число щелей дифракционной решетки, тем более резки главные максимумы. На рис. 19.15 представлены фотографии дифракционной картины, полученной от решеток с разным числом N щелей (постоянная дифракционной решетки одинакова), а на рис. 19.16 — график распределения интенсивности.

Особо отметим роль минимумов от одной щели. В направлении, отвечающем условию (19.27), каждая щель дает минимум, поэтому минимум от одной щели сохранится и для всей решетки. Если для некоторого направления одновременно выполняются условия минимума для щели (19.27) и главного максимума решетки (19.29), то соответствующий главный максимум не возникнет. Обычно стараются использовать главные максимумы, которые размещаются между первыми минимумами от одной щели, т. е. в интервале

При падении на дифракционную решетку белого или иного немонохроматического света каждый главный максимум, кроме центрального, окажется разложенным в спектр [см. (19.29)]. В этом случае k указывает порядок спектра.

Таким образом, решетка является спектральным прибором, поэтому для нее существенны характеристики, которые позволяют оценивать возможность различения (разрешения) спектральных линий.

Одна из таких характеристик — угловая дисперсия — определяет угловую ширину спектра. Она численно равна угловому расстоянию da между двумя линиями спектра, длины волн которых различаются на единицу (dl. = 1):

Дифференцируя (19.29) и используя только положительные значения величин, получаем

Из последних двух равенств имеем

Возможность различать близкие спектральные линии зависит не только от ширины спектра, или угловой дисперсии, но и от ширины спектральных линий, которые могут накладываться друг на друга.

Принято считать, что если между двумя дифракционными максимумами одинаковой интенсивности находится область, где суммарная интенсивность составляет 80% от максимальной, то спектральные линии, которым соответствуют эти максимумы, уже разрешаются.

При этом, согласно Дж. У. Рэлею, максимум одной линии совпадает с ближайшим минимумом другой, что и считается критерием разрешения. На рис. 19.17 изображены зависимости интенсивности I отдельных линий от длины волны (сплошная кривая) и их суммарная интенсивность (штриховая кривая). Из рисунков легко увидеть неразрешенность двух линий (а) и предельную разрешенность (б), когда максимум одной линии совпадает с ближайшим минимумом другой.

Разрешение спектральных линий количественно оценивается разрешающей способностью, равной отношению длины волны к наименьшему интервалу длин волн, которые еще могут быть разрешены:

R = l./ Dl.. (19.35)

Так, если имеются две близкие линии с длинами волн l₁ ³ l₂ , Dl = l₁ - l₂, то (19.35) можно приближенно записать в виде

Условие главного максимума для первой волны

С ним совпадает ближайший минимум для второй волны, условие которого

Приравнивая правые части последних двух равенств, имеем

откуда [с учетом (19.36)]

Итак, разрешающая способность дифракционной решетки тем больше, чем больше порядок k спектра и число N штрихов.

Рассмотрим пример. В спектре, полученном от дифракционной решетки с числом щелей N = 10 000, имеются две линии вблизи длины волны l = 600 нм. При какой наименьшей разности длин волн Dl эти линии различаются в спектре третьего порядка (k = 3)?

Для ответа на этот вопрос приравняем (19.35) и (19.37), l/Dl = kN, откуда Dl = l/(kN). Подставляя числовые значения в эту формулу, находим Dl = 600 нм/(3 • 10 000) = 0,02 нм.

Так, например, различимы в спектре линии с длинами волн 600,00 и 600,02 нм и не различимы линии с длинами волн 600,00 и 600,01 нм

Выведем формулу дифракционной решетки для наклонного падения когерентных лучей (рис. 19.18, b — угол падения). Условия формирования дифракционной картины (линза, экран в фокальной плоскости) те же, что и при нормальном падении.

Проведем перпендикуляры А'В кпадающим лучам и АВ' ко вторичным волнам, идущим под углом a к перпендикуляру, восставленному к плоскости решетки. Из рис. 19.18 видно, что к положению А¢В лучи имеют одинаковую фазу, от АВ' и далее разность фаз лучей сохраняется. Следовательно, разность хода есть

d = ВВ'-АА'. (19.38)

Из D АА'В имеем АА¢ = АВ sin b = с sin b. Из DВВ'А находим ВВ' = АВ sin a = с sin a. Подставляя выражения для АА¢ и ВВ' в (19.38) и учитывая условие для главных максимумов, имеем

с (sin a - sin b) = ± kl. (19.39)

Центральный главный максимум соответствует направлению падающих лучей (a= b).

Наряду с прозрачными дифракционными решетками используют отражательные, у которых штрихи нанесены на металлическую поверхность. Наблюдение при этом ведется в отраженном свете. Отражательные дифракционные решетки, изготовленные на вогнутой поверхности, способны образовывать дифракционную картину без линзы.

В современных дифракционных решетках максимальное число штрихов составляет более 2000 на 1 мм, а длина решетки более 300 мм, что дает значение N около миллиона.

Читайте также: