Что такое лямбда критическая в волноводе

Обновлено: 08.01.2025

Выясним условия существования тех или иных типов волн в зависимости от их индекса, ширины волновода и длины волны генератора . При этом будем исходить из сформулированного выше условия, которое на основании формул для суммарного поля между двумя плоскостями

где − индекс типа волны.

Действительно, при выполнении этого условия амплитудная синусоидальная функция, описывающая распределение поля в поперечном сечении волновода, обращается в нуль на верхней и нижней стенках (рисунок 14).

Рисунок 14 − Распространение волны в двухплоскостном волноводе

Это условие может быть переписано в следующем эквивалентном виде:

Рисунок 15 − Распространение при разной длине волны

Отсюда можно сделать вывод: при фиксированных параметрах и каждому индексу соответствует определенное значение угла падения , обеспечивающеее условие существования волн типов или (рисунок 15). Отметим при этом, что с ростом индекса угол падения должен уменьшаться.

Поскольку левая часть последнего соотношения ограничена в интервале , данное соотношение не может быть выполнено при любых , и . Действительно, для любого индекса найдется такая длина волны генератора, которую будем называть критической длиной волны данного типа и обозначать , для которой выполнение условий возможно лишь при максимальном значении , т.е.

Если теперь выбрать значение , то граничные условия на стенках волновода не могут быть выполнены ни при каком вещественном значении угла падения. Физически это означает невозможность существования колебания данного типа в виде бегущей волны. Явления, происходящие в волноводе на критической длине волны, могут быть сформулированы следующим образом. Поскольку , образуется стоячий волновой процесс в поперечной плоскости, т.е. никакого волнового движения, а следовательно, и передачи энергии вдоль оси не происходит. Однако важно подчеркнуть, что на критической длине волны

Теперь можно сформулировать основной вывод из приведенных рассуждений. Каждый тип колебаний с индексом может существовать как бегущая волна в области длин волн, удовлетворяющих равенству

Волны, более длинные, чем , по волноводу на данном типе колебаний распространяться не могут. Принято говорить, что область частот, удовлетворяющая неравенству , является областью отсечки данного типа колебаний.

Тип волны, обладающий наибольшей критической длиной, носит название основного (или низшего) в данном волноводе. Для рассматриваемого здесь двухплоскостного волновода низших типов волн два: это типы и , для них . Итак, если длина волны генератора превосходит удвоенную ширину волновода, то никакие волны Е- и Н-типов распространяться в нем не могут. Если , то в волноводе могут существовать лишь волны низших типов. При появляется возможность возникновения двух волн высших типов , и т.д.

Знание критической длины волны позволяет для конкретной длины волны генератора определить фазовую скорость на любом типе колебаний:

Аналогично находится длина волны в волноводе:

Формулы подобного вида будут часто встречаться в дальнейшем, при рассмотрении волноводов разного типа.

где − индекс типа волны.

Рисунок 14 − Распространение волны в двухплоскостном волноводе

Это условие может быть переписано в следующем эквивалентном виде:

Рисунок 15 − Распространение при разной длине волны

Аналогично находится длина волны в волноводе:

Формулы подобного вида будут часто встречаться в дальнейшем, при рассмотрении волноводов разного типа.

Классификация направляемых электромагнитных волн и направляющих систем .

Передачу энергии по длинной линии можно рассматривать так же как и распространение электромагнитных волн по направляющим системам, которыми, кроме двухпроводных линий, могут быть металлические, диэлектрические и полупроводниковые поверхности, трубки, стержни и т.д. Электромагнитные волны в направляющих системах движутся вдоль граничных поверхностей . Направляемые волны, подобно плоской электромагнитной волне, распространяются только в каком – то заданном направлении. Они делятся на поперечные, электрические, магнитные и смешанные. Названия определяются ориентацией векторов напряженности электрического Е и магнитного Н полей распространяющейся волны.

Поперечными, или волнами типа Т (от англ. transversal – поперечный), называются волны, у которых в направлении распространения энергии отсутствуют составляющие векторов Е и Н, то есть эти векторы лежат в плоскости, перпендикулярной направлению распространения энергии.

Электрическими, или волнами типа Е называются волны, у которых вектор Е имеет и поперечные и продольную составляющие, а вектор Н – только поперечные.

Магнитными, или волнами типа Н называются волны, у которых вектор Н имеет и поперечные и продольную составляющие, а вектор Е – только поперечные.

Смешанными, или гибридными типа НЕ или ЕН называются волны, у которых векторы Е и Н имеют как поперечные, так и продольные составляющие.

Для пояснения этого используем следующий пример. Пусть в некоторой направляющей системе энергия распространяется вдоль ось декартовой системы координат. Тогда оси , будут поперечными, так как они лежат в плоскости, перпендикулярной оси . В этом случае будем иметь: для волн Т ; для волн Е , ; для волн Н , ; для смешанных , .

Все направляющие системы делятся на два широких класса: открытого и закрытого типов. В линиях передачи открытого типа переносимая энергия распределена во всем окружающем линию пространстве. Чаще всего конструкции линий этого типа выполняют так, чтобы большая часть энергии электромагнитного поля была сосредоточена в непосредственной близости от линии. Примером линии открытого типа являются симметричные кабели. Эти линии подвержены влиянию среды и окружающих предметов, то есть в них практически всегда наблюдаются потери на излучения.

В линиях передачи закрытого типа вся передаваемая энергия сосредоточена в пределах объема, экранированного от окружающей среды металлической оболочкой той или иной формы. Из линий закрытого типа широко используются коаксиальные кабели. Линия этого типа является двухпроводной экранированной, а поэтому потери на излучение в ней отсутствуют.

По мере увеличения частоты электромагнитной энергии в коаксиальных линиях передачи растут потери в диэлектрике, поэтому они применяются до частот не более 1-3 ГГц. Если в коаксиальной линии убрать внутренний проводник, то не будет необходимости в жестком диэлектрике, который обеспечивает соосность проводника и экрана. Потери резко упадут. Но ток проводимости по одному проводу (металлической трубке – экрану) проходить не будет. На низких частотах передача электрической энергии при этом отсутствует. Однако при определенных условиях электромагнитные волны могут распространяться по полым металлическим трубам различной формы поперечного сечения, которые называются волноводами.

Процесс передачи энергии по волноводам эквивалентен радиопередаче, но здесь распространяется волна не во все стороны, а лишь в заданном направлении.

Физические процессы в волноводах.

Электромагнитное поле в волноводе. Рассмотрим двухпроводную линию , нагруженную на сопротивление, равное волновому.

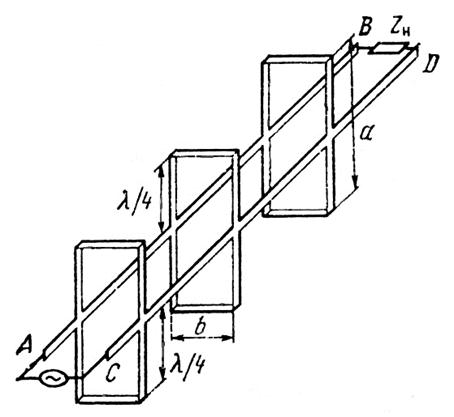
Пояснение принципа образования волновода.

В такой линии наблюдается режим бегущей волны. Для того чтобы закрепить провода и в воздухе, используем четвертьволновые короткозамкнутые шлейфы, расположенные на произвольных расстояниях друг от друга. Так как входное сопротивление таких шлейфов теоретически бесконечно, то их можно рассматривать как металлические изоляторы и они не нарушают работу исходной двухпроводной линии. Устремив число шлейфов к бесконечности, а расстояние между ними к нулю, получим конструкцию, которая называется прямоугольным волноводом.

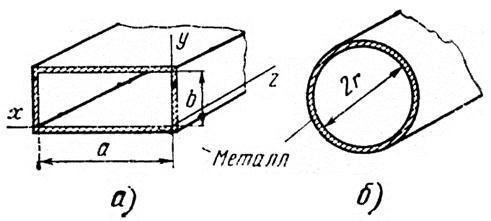
Металлические волноводы: а) – прямоугольный; б) – круглый.

Таким же образом можно перейти от двухпроводной линии к круглому волноводу. Только в этом случае металлическим изоляторам следует придать не прямоугольную, а круглую форму.

Режим работы волновода в сильной степени отличается от режима работы двухпроводной линии с согласованной нагрузкой. В волноводе, кроме бегущей волны, распространяющейся в направлении оси, будут существовать стоячие волны в поперечном сечении. Эти волны образуются за счет энергии, ответвляющейся от бегущей вдоль оси волны в металлический изолятор.

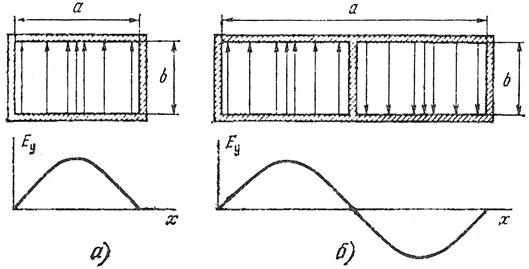
Структура поля в поперечном сечении волновода:

а) – волны типа ; б) – волны типа .

Густота силовых линий здесь характеризует напряженность (интенсивность) поля.

Критическая длина волны в волноводе.

Если изменить рабочую длину волны так, что размер широкой стенки волновода станет меньше , то передача энергии по волноводу прекратится, так как сопротивление металлических изоляторов резко уменьшится, увеличится количество ответвляющейся в них энергии, и уровень бегущей вдоль оси волны резко упадет. Поэтому, существует определенная длина волны , которая называется критической, при превышении которой распространение энергии вдоль волновода невозможно. Следовательно, для передачи энергии по волноводу требуется, чтобы рабочая длина волны , была меньше критической:

Критическая длина волны зависит от размеров волновода. Для прямоугольного волновода , то есть:

Типы волн в волноводе.

В волноводе могут существовать различные типы волн, отличающиеся структурой силовых линий, которые называются модами волновода. Для нахождения выражений, описывающих векторы поля Е и Н в волноводе, необходимо решить систему уравнений Максвелла с учетом геометрии конструкции. Полученная конкретная структура поля указывается индексами и , то есть волны обозначаются как , , , и т.д.

Число равно числу полуволн изменения интенсивности поля, укладывающихся вдоль широкой стенки волновода , число – числу полуволн изменения интенсивности поля, укладывающихся вдоль узкой стенки волновода . Для круглого волновода индекс характеризует число волн поля по периметру, а – полуволн по диаметру.

Структура силовых линий вектора Н для волн типа и показана на рисунке.

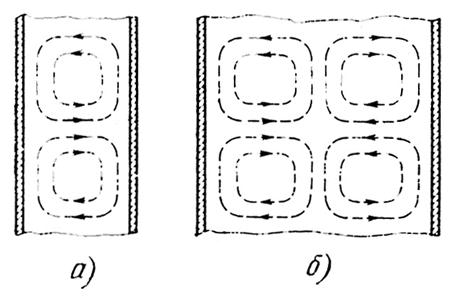
Магнитное поле в продольном сечении волновода:

а) – волны типа ; б) – волны типа .

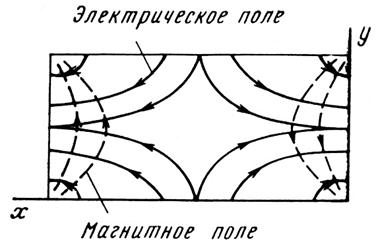
Структура поля волны типа в поперечном сечении прямоугольного волновода.

Зная тип волны, можно качественно построить картину поля в сечениях волновода и без применения формул для векторов поля Е и Н.

Волны различных типов отличаются не только структурой силовых линий. Различными у них являются и критические длины волны. Например, в прямоугольном волноводе:

Тип волны, критическая длина которой является наибольшей из всех возможных типов волн, называется основным типом волны, или основной волной (модой) данного волновода.

Применение волноводов.

Волноводы используются в различных радиотехнических устройствах в качестве фидеров, колебательных систем, называемых объемными резонаторами, фильтров, линий связи и т.д.

Фидеры. На частотах выше 1 ГГц для передачи электроэнергии от радиопередатчика к антенне или от антенны к приемнику в качестве фидера повсеместно используются волноводы. Поскольку фидер должен иметь малые собственные потери, внутренние стенки волновода тщательно шлифуются и покрываются слоем серебра. Этим и отсутствием изоляторов внутри волновода достигаются потери, значительно меньшие, чем в коаксиальных фидерах.

По волноводному фидеру можно передавать значительно большую энергию, чем по коаксиальному фидеру тех же размеров.

Волноводные линии связи. Возможность работы на высоких частотах (десятки гигагерц), большая широкополосность (сотни мегагерц), малое затухание явились предпосылками для использования металлических волноводов в качестве линий связи в сверхширокополосных многоканальных системах. Однако были построены только экспериментальные линии, так как экономически они оказались невыгодными. Более широкое применение нашли световодные волноводы.

Объемные резонаторы. Колебательная система может быть построена на базе волноводов прямоугольной и круглой формы.

Для перестройки волноводных резонаторов одна из короткозамыкающих волновод пластин выполняется в виде подвижного поршня. Возбуждение резонаторов и отвод энергии от них осуществляется так же, как и в волноводах, – с помощью штыря, рамки или отверстия связи.

Отличительной особенностью объемных резонаторов является высокая добротность, а следовательно, высокая фильтрующая способность их, как колебательных систем, и высокая стабильность резонансных частот. Величина добротности, в зависимости от конструкции, диапазона частот, тщательности обработки внутренней поверхности резонатора, колеблется от нескольких тысяч до нескольких сотен тысяч.

Основным недостатком объемных резонаторов является наличие множества резонансных частот.

Наибольшая длина волны в свободном пространстве, выше которой распространение данного типа волн в волноводе невозможно.

критическая частота — Наименьшая частота, при которой возможно распространение данного типа волны в линии передачи.

Способы отыскания мест негерметичности оболочек кабелей.

17.116. Место негерметичности оболочки кабеля определяют в два этапа: сначала определяют район негерметичности, а затем уточняют место негерметичности.

17.117. Район негерметичности оболочки кабеля определяют манометрическим методом или по расходу воздуха, подаваемого с обоих концов участка кабеля, при установившемся режиме давления в кабеле.

Причины разницы пропускной способности многомодовых и одномодовыхсветоводов.

Одномодовое и многомодовое волокна

Как уже отмечалось, существует два типа оптоволоконного кабеля: одномодовый и многомодовый. Основное отличие между ними заключается в толщине сердечника и оболочки. Одномодовыйсветовод обычно имеет толщину порядка 8/125 микрон, а многомодовое волокно 50/125 микрон. Эти значения соответствуют диаметру сердечника и диаметру вместе взятых: сердечника и оболочки.

Световой луч, распространяющийся по сравнительно тонкому сердечнику одномодового кабеля, отражается от оболочки не так часто, как это происходит в более толстом сердечнике многомодового кабеля. Для передачи данных в последнем применяется полихромный (многочастотный) свет, а в одномодовом используется свет только одной частоты (монохромное излучение), отсюда они и получили свои названия. Сигнал, передаваемый одномодовым кабелем, генерируется с помощью лазера, и представляет собой волну, естественно, одной длины, в то время как многомодовые сигналы, генерируемые светодиодом (LED – LightEmittedDiode), переносят волны различной длины. В одномодовом кабеле затухания сигнала (потери мощности сигнала) практически исключены. Это и ряд выше перечисленных качеств позволяют одномодовому кабелю функционировать с большей пропускной способностью по сравнению с многомодовым кабелем и преодолевать расстояния в 50 раз длиннее.

С другой стороны, одномодовый кабель намного дороже и имеет сравнительно большой радиус изгиба по сравнению с многомодовым оптическим кабелем, что делает работу с ним неудобной. Большинство оптоволоконных сетей используют многомодовый кабель, который хотя и уступает по производительности одномодовому кабелю, но зато значительно эффективней, чем медный. Телефонные компании и кабельное телевидение, тем не менее, стремятся применять одномодовый кабель, так как он может передавать большее количество данных и на более длинные дистанции.

Обухова ГМ

Маком-МХ

Гибкий мультиплексор

Гибкий мультиплексор предназначен для формирования первичных цифровых потоков со скоростью 2048 кбит/с (поток Е1) из аналоговых речевых сигналов и сигналов цифровых интерфейсов, электронной кроссовой коммутации цифровых каналов со скоростью 64 кбит/с, передачи цифровых потоков по сети IP/Ethernet, а также для конвертации физических стыков и линейной сигнализации.

Оборудование имеет следующие типы интерфейсов:

цифровые стыки Е1, кодировка HDB3 или AMI;

цифровые синхронные стыки V.24, V.11, V.35, V.36, X.21;

FXS (двухпроводные физические линии для подключения оконечных абонентских устройств со шлейфной сигнализацией);

трехпроводные физические соединительные линии (СЛ) с сигнализацией батарейным способом;

двух-/четырех-/шестипроводные окончания каналов ТЧ аппаратуры систем передачи;

двухпроводные физические линии системы МБ;

цифровые асинхронные стыки V.24; цифровые стыки ИКМ-15 (1024 кбит/с);

цифровые сонаправленные стыки 64 кбит/с (G.703.1);

FXO (двухпроводные физические линии, включаемые в абонентские комплекты АТС);

Ethernet 10/100 Base-T;

ВОЛС Ethernet TDMoP;

цифровые стыки SHDSL.

Конструктивное исполнение:

Оборудование реализовано в виде модульной конструкции, при этом модули блока питания (БП) и центрального процессора (ЦП) являются базовыми и устанавливаются при любой конфигурации аппаратуры. Модуль ЦП осуществляет кроссовую коммутацию ОЦК и сигнальных каналов, производит конвертирование протоколов сигнализации, управляет работой модулей периферии. Параметры конфигурации хранятся в энергонезависимой памяти.

Сопряжение аппаратуры с подключаемыми каналами и линиями обеспечивают модули периферийных окончаний (модули периферии). Каждый модуль периферии содержит однотипные комплекты, обеспечивающие подключение определенных каналов и линий. Питание оборудования осуществляется от сети постоянного тока с заземленным положительным полюсом и напряжением 24…60В. Конструктивно каждый модуль выполнен в виде отдельного ТЭЗа. ТЭЗы устанавливаются в 19” евроконструктив 3U84ТЕ в стоечном исполнении. Общее количество модулей периферии, которое можно установить в один корпус, составляет 16. Все посадочные места модулей периферии – универсальны.

Варианты применения:

В простейшем случае, с помощью мультиплексора Маком-МX можно скоммутировать от 4 до 60 аналоговых окончаний на один-два цифровых потока Е1 или до 128 абонентских комплектов на 4 потока Е1. В качестве аналоговых окончаний могут выступать 2, 4 или 6 проводные линии ТЧ, с внутриполосной сигнализацией или с сигнализацией выделенному сигнальному каналу, абонентские линии или абонентские комплекты. Информация речевых каналов при этом может быть сжата до 32 или 16 кбит/с на канал, используя кодирование АДИКМ.

Мультиплексор используется для организации цифрового канала связи по технологии SHDSL/SHDSL.bis со скоростью до 11,4 Mbps. В качестве особых возможностей мультиплексора следует отметить функции конвертора протоколов.

С помощью мультиплексора можно осуществлять конвертацию в обе стороны:

местной и междугородной зоновой сигнализации 2600 Гц по каналам ТЧ в Е1 протокол 2ВСК;

одночастотной сигнализации в 1ВСК;

сигнализации батарейным способом по трёхпроводным соединительным линиям в Е1 протокол 2ВСК;

преобразование стыка ИКМ-15 в Е1.

Также мультиплексор позволяет, устанавливать широковещательные соединения, т.е. подать сигнал с одного из аналоговых или цифровых каналов на несколько других. Применяется в частности для подачи программ радиовещания в несколько пунктов одновременно.

Конфигурирование и мониторинг:

Имеется возможность удаленного конфигурирования и мониторинга мультиплексора через потоки Е1, DSL, что позволяет объединить несколько мультиплексоров в сеть и управлять их работой удаленно с помощью компьютера, подключенного к любому из мультиплексоров этой сети. Программное обеспечение для центра эксплуатации работает в среде Windows 98/2000/XP и позволяет производить мониторинг /настройку работы как локального оборудования по стыку RS-232, так и сети мультиплексоров через цифровые тракты E1.

В радиотехнической практике особое значение приобретает задача направленной передачи энергии электромагнитных волн от генератора к потребителю. В качестве основных требований, которые при этом предъявляются, выступают минимум потерь при передаче и максимум передаваемой мощности. Поставленная задача решается с помощью специальных направляющих устройств, носящих название линий передачи. В данном разделе будет рассмотрено несколько типов линий передачи, используемых в диапазоне частот 30 МГц – 30 ГГц, и будут исследованы механизмы распространения в них электромагнитных волн. Основное внимание уделено линиям передачи в виде полых металлических труб, различного поперечного сечения (волноводам) и коаксиальным линиям передачи.

Цель данной лекции является изучение направляемых электромагнитных волн в круглом и коаксиальном волноводах.

Круглый волновод

В первом вопросе лекции рассматривается решение уравнений Максвелла применительно к полым волноводам круглого сечения, изучаются основные свойства и структура направляемых волн в круглом волноводе.

Рис. 1 – Круглый волновод

В этом случае 1-ое и 2-ое уравнения Максвелла примут вид:

Для круглого волновода удобнее ввести цилиндрическую систему координат (r, j, z) и искать решение данных уравнений в этой системе координат. Порядок решения уравнений аналогичен тому, как в случае прямоугольного волновода:

1) Раскрывается операция rot в цилиндрической системе координат.

2) Все поперечные составляющие поля (т.е. Е_r, Е_j, Н_r, Н_j) выражаются через продольные Е_z и Н_z.

3) Составляется дифференциальное уравнение для продольных составляющих и находится его решение.

Как и в прямоугольном волноводе, в круглом волноводе могут существовать как Е, так и Н – волны. Рассмотрим сначала Е – волны. По определению, для таких волн: Н_z = 0, все остальные составляющие не равны 0.

Составим дифференциальное уравнение для амплитудного значения продольной составляющей Е_z_m:

где: g 2 = k 2 - b 2 – поперечное волновое число; k – постоянная распространения волны в неограниченном (свободном) пространстве; b - постоянная распространения волны в круглом волноводе; Ñ 2 – поперечный оператор Лапласа.

Раскрывая Ñ 2 в цилиндрической системе координат, получим:

Решая это дифференциальное уравнение методом разделения переменных, получим:

где: Е₀ – некоторая постоянная; J_n – функция Бесселя n – го порядка, n=0,1,2,…

Теперь накладываем граничные условия: касательная составляющая электрического поля должна быть равна 0 на стенках волновода, т.е. Е_j = 0 при r = R. Это означает, что и Е_z_m должна быть равна нулю при r = R, т.е:

Чтобы данное требование выполнялось при любом угле j, необходимо, чтобы выполнялось условие:

J_n(gR) = 0. (1 а)

Функции Бесселя различного порядка изображены на графике рис. 2.

Рис. 2 – Функции Бесселя

Из графиков видно, что для выполнения условие (1 а) необходимо, чтобы:

gR = V_nm , (1 б)

где: V_nm – m – ый корень функции Бесселя n – го порядка.

Из (1 б) получаем, что поперечное волновое число:

Следовательно, амплитудное значение продольной составляющей:

а мгновенное значение:

При известной Е_z, далее определяются все остальные составляющие поля Е – волны: E_z, E_φ, H_r, H_φ.

Проведем анализ полученного уравнения (2).

1) Направляемая волна Е – типа распространяется по круглому волноводу вдоль оси z с постоянной распространения β. Каждой паре чисел m и n соответствует своя структура электромагнитного поля, которая обозначается как Е_nm. Из графиков на рис. 2 видно, что наименьшим корнем функции Бесселя является корень V₀₁, следовательно простейшей волной Е – типа является волна Е₀₁.

2) Определим постоянную распространения β для Е_nm волн.

Аналогично, как и для прямоугольного волновода получаем:

- если k 2 > γ 2 , то β – вещественная величина и, следовательно, электромагнитная волна Е_nm будет распространяется в круглом волноводе;

- граничный случай возникает когда:

k 2 = γ 2 или .

Длина волны, отвечающая этому условию, называется критической длиной волны в круглом волноводе:

Определим длину волны в круглом волноводе.

Поскольку , или: , то:

Заметим, что выражение (3) имеет тот же вид, что и для прямоугольного волновода.

Определим фазовую V_ф и групповую V_гр скорости Е – волны в круглом волноводе:

Так как V_ф× V_гр= с 2 , то:

Рассмотрим теперь Н – волны в круглом волноводе. Для этих волн по определению составляющая Е_z=0, все остальные составляющие не равны нулю. Составим дифференциальное уравнение для амплитудного значения продольной составляющей Н_z_m:

Решение этого уравнения имеет вид:

Накладываем граничные условия: Е_φ = 0 при r = R. Это означает, что производная составляющей H_zm при r = R должна быть равна нулю, т.е:

Для выполнения данного условия при любом j, необходимо чтобы:

J_n¢(gR)=0. (4)

Первая производная любой функции – это есть точки максимума или минимума этой функции. Поэтому (см. рис. 2), чтобы выполнялось условие (4), необходимо потребовать:

где: U_nm – m-ый корень производной функции Бесселя n-го порядка.

Следовательно, из (5) волновое число g для Н – волн в круглом волноводе:

Тогда мгновенное значение продольной составляющей Н_z равно:

Анализ полученного уравнения показывает, что каждой паре чисел m и n соответствует своя структура поля Н – волны в круглом волноводе, которая обозначается как Н_mn. Из графиков на рис. 2 видно, что первым корнем является корень U₁₁, Поэтому простейшей волной Н – типа будет волна Н₁₁.

Критическая длина волны Н – типа определяется из условия: k 2 =g 2 .

Поскольку корень U₁₁ является наименьшим из всех возможных корней функции Бесселя, то l_кр волны Н₁₁ будет наибольшей из всех Н_nm и Е_nm типов волн. Это означает, что одномодовый режим работы круглого волновода возможен только на волне Н₁₁. Вывод формул для l_в, V_ф, и V_гр аналогичен тому, как это проводилось для Е – волн и не представляется сложным при самостоятельном изучении.

Использование круглых волноводов в качестве линии передачи

В этом вопросе рассматриваются особенности применения круглых волноводов в качестве линий передачи СВЧ мощности.

В круглом волноводе, в отличие от прямоугольного волновода, в качестве основного типа колебания, используется один из трех типов волн: Н₁₁, Е₀₁ или Н₀₁. Рассмотрим особенности этих волн, обусловливающих их применение на практике.

а) Обратимся к структуре электромагнитных волн этих волн, изображенных на рис. 3, и распределению линий поверхностного тока, показанных на рис. 4. Отметим, что у волны Н₀₁ в отличии от волн Н₁₁ и Е₀₁ отсутствует продольная составляющая тока проводимости (существуют только поперечные, кольцевые токи).

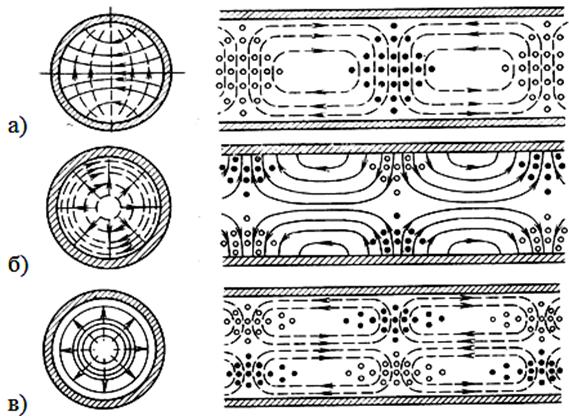
Рис. 3 – Структура волн Н₁₁ (а), Е₀₁(б) и Н₀₁ (в) в круглом волноводе

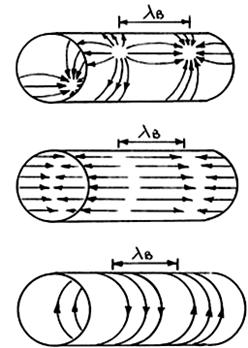
Рис. 4 – Распределение линий поверхностного тока для волн Н₁₁ (а), Е₀₁(б) и Н₀₁ (в)

б) Критическая длина волны для колебаний Е– и Н–типа в круглом волноводе определяется выражениями:

где: R – радиус круглого волновода; V_nm – m-ый корень функции Бесселя n-го рода; U_nm – m-ый корень производной функции Бесселя n-го рода.

В табл. 1 приведены значения l_кр первых шести типов колебаний в круглом волноводе.

Тип волны	Н₁₁	Е₀₁	Н₂₁	Е₁₁	Н₁₁	Н₃₁
l_кр/R	3,42	2,61	2,06	1,64	1,64	1,46

На рис. 5 приведены зависимости коэффициента затухания a в круглом волноводе от частоты и допустимой мощности Р от частоты для рассматриваемых трех типов волн.

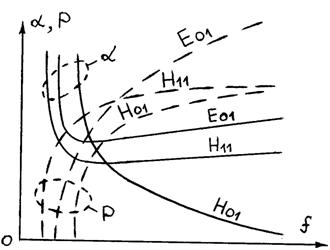
Рис. 5 – Зависимость a и Р от частоты

На основании рис. 3, 4, 5 и табл. 1 несложно сформулировать следующие особенности волн Н₁₁, Е₀₁ и Н₀₁:

1) Данный тип колебаний обладает наибольшей l_кр. Следовательно, только на волне Н₁₁ возможен одномодовый режим работы круглого волновода без применения каких-либо дополнительных мер;

2) Структура электромагнитного поля данной волны является несимметричной относительно произвольной поперечной оси (см. рис. 3). Вследствие этого, при движении волны вдоль круглого волновода происходит изменение поляризации волны, как показано на рис. 6.

3) Чтобы зафиксировать плоскость поляризации, на практике прибегают к изменению поперечного сечения круглого волновода, используя эллипс, и переходя таким образом к эллиптическим волноводам (см. рис. 7);

4) Из всех трех типов волн, волна Н₁₁ обладает наибольшей допустимой рабочей мощностью.

Рис. 6 – Изменение плоскости Рис. 7 – Эллиптический

поляризации волны Н₁₁ волновод

1) Волна является осесимметричной (см. рис. 3), поэтому является чрезвычайно удобной в качестве волны, используемой для передачи электромагнитной энергии в круглом волноводе или для применения в функциональных устройствах на основе круглого волновода (СВЧ фильтры, вращающиеся соединения и т.д.);

2) Волна существует наряду с Н₁₁, следовательно, для предотвращения потерь электромагнитной энергии требуется принятие специальных мер для подавления волны Н₁₁.

1) У данной волны отсутствуют поперечные составляющие поверхностного тока на стенках волновода (имеются только круговые токи), см. рис. 5. Это приводит к тому, что при увеличении произведения R×¦ коэффициент затухания a данной волны стремится к нулю (см. рис. 5);

2) Наряду с волной Н₀₁ существуют еще по крайней мере четыре типа колебаний (см. табл. 1). В этой связи весьма сложно обеспечить подавления этих паразитных типов колебаний, чтобы добиться тем самым режима с наименьшим коэффициентом затухания электромагнитной энергии в круглом волноводе с волной Н₀₁.

Коаксиальный волновод

В данном вопросе приводится решение уравнений Максвелла применительно к коаксиальной линии передачи.

Коаксиальным волноводом называется направляющая система, образованная двумя изолированными друг от друга соосными, металлическими круглыми проводниками диаметрами 2a и 2b (см. рис. 8).

Рис. 8 – Коаксиальный волновод

Предположим, что волновод заполнен однородной изотропной средой с параметрами e_a, m_a и без потерь (s=0). Пусть сторонние токи отсутствуют, в этом случае 1-ое и 2-ое уравнения Максвелла принимают вид:

Из этих уравнений несложно получить волновые уравнения Гельмгольца:

где: – оператор Лапласа; - постоянная распространения в неограниченной среде с параметрами e_а, m_а.

Выберем в качестве направления распространения волны в коаксиальном волноводе ось z, тогда:

где: b - постоянная распространения в коаксиальном волноводе.

Подставив (6) в уравнение Гельмгольца, получим для напряженности электрического поля следующие выражения:

где: - поперечный оператор Лапласа; (k 2 - b 2 ) = g 2 – поперечное волновое число.

Характерной особенностью коаксиального волновода является то, что в отличие от прямоугольного и круглого волноводов, в нем могут распространяться три вида направляемых волн:

1) Поперечные (ТЕМ – волны).

2) Электрические (Е – волны).

3) Магнитные (Н – волны).

Для существования ТЕМ – волн в коаксиальном волноводе (т.е. волн, у которых отсутствуют составляющие Е_z и Н_z), как следует из уравнения (7), необходимо выполнение условия:

g 2 = k 2 – b 2 = 0. (8)

Из этого условия следуют два важных вывода:

1) b 2 = k 2 , или , или l_В = l,

где: l_В – длина волны в коаксиальном волноводе; – длина волны в неограниченной среде с параметрами e_a и m_a.

Таким образом, длина волны в коаксиальном волноводе равна длине волны в неограниченном пространстве.

2) Т.к. , то l_кр = ¥ (f_кр = 0),

где: l_кр, f_кр – критическая длина волны и критическая частота в коаксиальном волноводе.

Это означает, что в коаксиальном волноводе, в отличии от прямоугольного и круглого волновода, сигнал с любой частотой может переносится ТЕМ–волной.

Поэтому, выбором геометрических размеров a и b коаксиального волновода, на практике всегда добиваются того, чтобы мощность сигнала переносилась только ТЕМ – волной. В связи с этим, рассмотрим более подробно распространение ТЕМ – волн в коаксиальном волноводе.

Из уравнения (7) с учетом (8) имеем:

Для коаксиального волновода решение данного уравнения проще всего искать в цилиндрической системе координат (r, j, z). Уравнение вида (9) в математике называется уравнением Лапласа, которое имеет следующее решение:

где: U – некоторая скалярная функция, подлежащая определению. Определим ее, используя известное из математики тождество: div grad U = 0. Раскрывая операцию div grad в цилиндрической системе координат, получим:

Накладываем граничные условия: касательная составляющая электрического поля Е_j должна быть равна нулю при r = a и r = b. Т.к. , то это означает, что при r = a и r = b. Тогда имеем:

При найденном U определяем комплексные значения составляющих электрического поля ТЕМ – волны в коаксиальном волноводе:

Составляющие магнитного поля определяем с помощью второго уравнения Максвелла:

Раскрывая операцию rot в цилиндрической системе координат, получим:

Таким образом, составляющие электромагнитного поля ТЕМ – волны в коаксиальном волноводе имеют вид:

На основании уравнений (10) на рис. 9 изображена структура поля ТЕМ–волны в коаксиальном волноводе.

Рис. 9 – Структура поля ТЕМ–волны в коаксиальном волноводе

© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.037)

Читайте также: