На графике представлен цикл теплового двигателя определите работу совершаемую газом

Обновлено: 07.01.2025

Тепловые двигатели. Термодинамические циклы. Цикл Карно

Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):

Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A₁, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A₂, равную по модулю площади под кривой cda. Полная работа за цикл A = A₁ + A₂ на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.

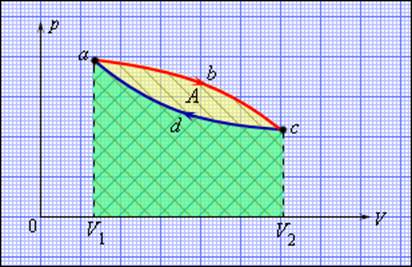
Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂ < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно

При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,

Работа A, совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты Q. Отношение работы A к количеству теплоты Q₁, полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия η тепловой машины:

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Энергетическая схема тепловой машины изображена на рис. 3.11.2.

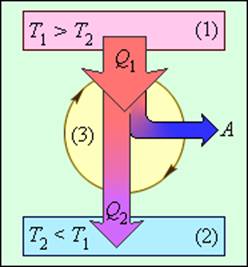
Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q₁ > 0, A > 0, Q₂ < 0; T₁ > T₂

В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.

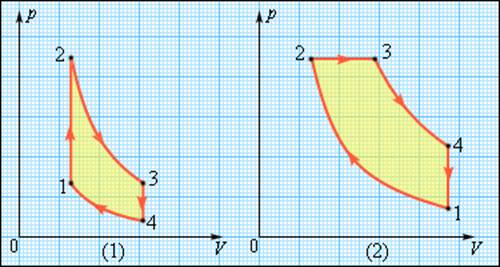
Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)

В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).

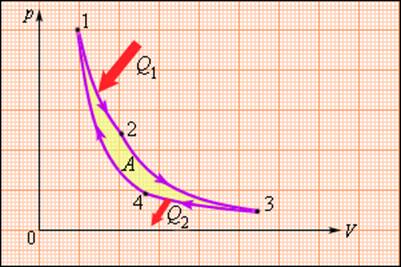
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится некоторое количество теплоты Q₁ = A₁₂. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при адиабатическом расширении падает до значения T₂. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T₂ < T₁. Происходит процесс изотермического сжатия. Газ совершает работу A₃₄ < 0 и отдает тепло Q₂ < 0, равное произведенной работе A₃₄. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T₁, газ совершает работу A₄₁ < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:

На диаграмме (p, V) эта работа равна площади цикла.

Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).

Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газа

где T₁ и T₂ – начальная и конечная температуры газа.

Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам

По определению, коэффициент полезного действия η цикла Карно есть

С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T₁ и холодильника T₂:

Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:

Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине, когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной.

В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме (p, V) обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.

Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q₂| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением

т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении β_х может быть и больше, и меньше единицы. Для обращенного цикла Карно

Если полезным эффектом является передача некоторого количества тепла |Q₁| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность β_Т теплового насоса может быть определена как отношение

т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:

следовательно, β_Т всегда больше единицы. Для обращенного цикла Карно

На графике представлен цикл теплового двигателя определите работу совершаемую газом

Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом . В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами .

Как следует из первого закона термодинамики, полученное газом количество теплоты полностью превращается в работу при изотермическом процессе, при котором внутренняя энергия остается неизменной ():

Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически . Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл , при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме () газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу , равную площади под кривой , при сжатии газ совершает отрицательную работу , равную по модулю площади под кривой . Полная работа за цикл на диаграмме () равна площади цикла. Работа положительна, если цикл обходится по часовой стрелке, и отрицательна, если цикл обходится в противоположном направлении.

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем , а с более низкой – холодильником . Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты и отдает холодильнику количество теплоты . Полное количество теплоты , полученное рабочим телом за цикл, равно

При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (). Согласно первому закону термодинамики,

Отсюда следует:

Работа , совершаемая рабочим телом за цикл, равна полученному за цикл количеству теплоты . Отношение работы к количеству теплоты , полученному рабочим телом за цикл от нагревателя, называется коэффициентом полезного действия тепловой машины:

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть () была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (). Энергетическая схема тепловой машины изображена на рис. 3.11.2.

В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (, ) и двух адиабат (, ). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (, ), одной изобары () и одной изохоры (). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке () газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру . Газ изотермически расширяется, совершая работу , при этом к газу подводится некоторое количество теплоты . Далее на адиабатическом участке () газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу . Температура газа при адиабатическом расширении падает до значения . На следующем изотермическом участке () газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре . Происходит процесс изотермического сжатия. Газ совершает работу и отдает тепло , равное произведенной работе . Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения , газ совершает работу . Полная работа , совершаемая газом за цикл, равна сумме работ на отдельных участках:

На диаграмме () эта работа равна площади цикла.

Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли его внутренней энергии. Для 1 моля газа

где и – начальная и конечная температуры газа.

По определению, коэффициент полезного действия цикла Карно есть

С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя и холодильника :

Любой участок цикла Карно и весь цикл в целом может быть пройден в обоих направлениях. Обход цикла по часовой стрелке соответствует тепловому двигателю, когда полученное рабочим телом тепло частично превращается в полезную работу. Обход против часовой стрелки соответствует холодильной машине , когда некоторое количество теплоты отбирается от холодного резервуара и передается горячему резервуару за счет совершения внешней работы . Поэтому идеальное устройство, работающее по циклу Карно, называют обратимой тепловой машиной .

В реальных холодильных машинах используются различные циклические процессы. Все холодильные циклы на диаграмме () обходятся против часовой стрелки. Энергетическая схема холодильной машины представлена на рис. 3.11.5.

Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением
т. е. эфективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на затраченной работы. При таком определении может быть и больше, и меньше единицы. Для обращенного цикла Карно

На графике представлен цикл теплового двигателя определите работу совершаемую газом

Относится ли ружьё к тепловым двигателям? Да, так как при выстреле внутренняя энергия топлива превращается в механическую энергию.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1. Определите КПД двигателя автомобиля, которому для выполнения работы 110,4 МДж потребовалось 8 кг бензина.

Задача № 2. Определите КПД двигателя автомобиля, которому для выполнения работы 220,8 МДж потребовалось 16 кг бензина.

Задача № 3. Определите КПД двигателя автомобиля, которому для выполнения работы 27,6 МДж потребовалось 2 кг бензина.

Задача № 4. На теплоходе установлен дизельный двигатель мощностью 80 кВт с КПД 30%. На сколько километров пути ему хватит 1 т дизельного топлива при скорости движения 20 км/ч? Удельная теплота сгорания дизельного топлива 43 МДж/кг.

Задача № 5. Патрон травматического пистолета «Оса» 18 x 45 мм, содержит резиновую пулю массой 8,4 г. Определите КПД патрона, если пуля при выстреле приобрела скорость 140 м/с. Масса порохового заряда патрона составляет 0,18 г, удельная теплота сгорания пороха 3,8 • 10 6 Дж/кг.

Задача № 6. Первый гусеничный трактор конструкции А. Ф. Блинова, 1888 г., имел два паровых двигателя. За 1 ч он расходовал 5 кг топлива, у которого удельная теплота сгорания равна 30 • 10 6 Дж/кг. Вычислите КПД трактора, если мощность двигателя его была равна около 1,5 кВт.

Задача № 7. Двигатель внутреннего сгорания совершил полезную работу, равную 2,3 • 10 4 кДж, и при этом израсходовал бензин массой 2 кг. Вычислите КПД этого двигателя.

Задача № 8. За 3 ч пробега автомобиль, КПД которого равен 25%, израсходовал 24 кг бензина. Какую среднюю мощность развивал двигатель автомобиля при этом пробеге?

Задача № 9. Двигатель внутреннего сгорания мощностью 36 кВт за 1 ч работы израсходовал 14 кг бензина. Определите КПД двигателя.

Задача № 10. ОГЭ Идеальная тепловая машина, работающая по циклу Карно, 80 % теплоты, полученной от нагревания, передаёт охладителю. Количество теплоты, получаемое рабочим телом за один цикл от нагревателя, Q₁ = 6,3 Дж. Найти КПД цикла ɳ и работу А, совершаемую за один цикл.

Задача № 11. ЕГЭ Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдаёт за один цикл охладителю количество теплоты Q₂ = 13,4 кДж. Найти КПД цикла ɳ.

Краткая теория для решения Задачи на КПД тепловых двигателей.

Задание 30 ЕГЭ по физике

Это задание также относится к высокому уровню сложности. Как правило, тематика этого задания «МКТ» и «Термодинамика». Какие-то задачи требуют только формульного решения, какие-то необходимо сопровождать графическими пояснениями термодинамических процессов. В любом случае, теоретический материал полностью соответствует кодификатору элементов содержания и спецификации контрольных измерительных материалов.

Запишем первый закон термодинамики для изобарного процесса:

Выразим из этого равенства изменение внутренней энергии:

Работу газа в изобарном процессе можно рассчитать по формуле:

с учетом уравнения Менделеева-Клапейрона получим:
(2).
При совершении работы давление бензола не изменяется, так как поршень в цилиндре легкоподвижный. Давление бензола все время остается равным атмосферному.

При этом
– масса бензола, превратившегося в газообразное состояние.

Количество теплоты, которое идет на превращение бензола в это состояние можно рассчитать по формуле:

Выражение для работы бензола (2) и количества теплоты (3) подставим в уравнение (1).

После сокращения на получим искомую формулу:

Подставим численные значения и проведем расчет:

Секрет решения. На первый взгляд задача кажется несложной, но в ней «спрятаны» несколько искусственных приемов, до которых додуматься достаточно сложно. Первый прием – выражение Это математический ход, который сразу подсказывает, что конкретно надо находить в этой задаче.

Второй прием – получение равенства, используя уравнения Менделеева-Клапейрона Здесь надо придерживаться следующих рассуждений: если в левой части уравнения есть переменная величина (в этой задаче ), то и в правой части должна изменяться какая-то физическая величина (в этой задаче ). Можно сказать еще проще: если в левой части равенства есть знак дельта " ", то и в правой части он должен обязательно появиться. В крайнем случае, можно «перебрать» все величины из правой части: температура не может изменяться, так как при парообразовании она всегда постоянна; молярная масса также неизменна, потому что речь идет об одном и том же газе; R – табличная величина. Остается только Эти рассуждения помогут понять ситуацию, описанную в задаче и правильно ее решить.

2. Одно и то же постоянное количество одноатомного идеального газа расширяется из одного и того же начального состояния до одного и того же конечного объёма первый раз по изобаре 1–2, а второй по адиабате 1–3 (см. рисунок). Отношение работы газа в процессе 1–2 к работе газа в процессе 1–3 равно =к=2. Чему равно отношение х количества теплоты полученного газом от нагревателя в ходе процесса 1–2, к модулю изменения внутренней энергии газа в ходе процесса 1–3?

Для участка 1–2 применим первый закон термодинамики с учетом изобарного процесса.

Работу газа при расширении найдем как площадь прямоугольника под графиком.

Изменение внутренней энергии одноатомного идеального газа запишем в виде формулы:

Применим уравнение Менделеева-Клапейрона:

Тогда (3) примет вид:

Таким образом количество теплоты на участке 12 равно:

Для участка 1–3 применим первый закон термодинамики с учетом адиабатного процесса.

но так как запишем:

или Это выражение означает, что газ на участке 13 совершает работу за счет уменьшения своей внутренней энергии.

Учтем, что по условию =к=2, тогда:

Используя (5) и (6) получим искомую формулу:

Секрет решения. Несмотря на громоздкие расчеты и обилие разных индексов в уравнениях, задача является среднего уровня сложности. Надо знать:

- первый закон термодинамики;

- его применение к изопроцессам;

- формулы, выражающие работу газа и его внутреннюю энергию (только для одноатомного идеального газа);

- уметь «читать» графики;

- понимать, что при расширении газ совершает положительную работу, при сжатии – отрицательную работу;

- проводить рассуждения о том, откуда газ берет энергию для совершения работы (за счет своей внутренней энергии или за счет поступления энергии извне);

- указанные пункты описывать соответствующими уравнениями.

Суть любой задачи по физике – описание физических процессов математическими уравнениями, которые надо решить удобным (рациональным) способом.

3. В тепловом двигателе 1 моль одноатомного разряженного газа совершает цикл 1–2–3–4–1, показанный на графике в координатах p–T, где p – давление газа, Т – абсолютная температура. Температуры в точках 2 и 4 равны и превышают температуру в точке 1 в 2 раза. Определите КПД цикла.

КПД теплового двигателя определяется формулой:

– полезная работа, совершенная газом за цикл, Q – полученное за цикл количество теплоты. Можно графически рассчитать работу, если перерисовать данный цикл в координатах рV. Проведем анализ каждого процесса.

В координатах рV график будет иметь вид:

Работа газа за цикл будет определяться площадью прямоугольника 1-2-3-4.

Поэтому (на основании закона Шарля).

(на основании закона Гей-Люссака).

Таким образом, можно выразить полезную работу через и

Газ получает положительное количество теплоты на участках 1–2 и 2–3.

Применим к этим участкам первый закон термодинамики.

Но работа газа на этом участке равна нулю, так как процесс изохорный.

С учетом уравнения Менделеева-Клапейрона и получим:

Для участка 23 первый закон термодинамики примет вид:

Работа определяется площадью прямоугольника под участком 23.

С учетом уравнения Менделеева-Клапейрона (4) примет вид:

Таким образом, полученное количество теплоты на участке 23 равно:

Общее количество теплоты, полученное за цикл:

Полученные выражения из (1) и (6) подставим в формулу КПД.

Секрет решения. За задачи на определение КПД тепловой машины по графику надо получать максимальные 3 балла. Эти задания сопровождаются большими расчетами, поэтому на первое место надо ставить внимательность их выполнения.

Необходимо выделить следующие моменты в решении:

- определять работу графически можно только в координатах рV;

- если в условии дан график в других координатах, то его надо перечертить в рV;

- поэтапно применять первый закон термодинамики и газовые законы для всех процессов;

Работа газа и КПД цикла

КПД тепловой машины можно вычислить как

Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:

Работа численно равна площади, ограниченной циклом. Поэтому

Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно

Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :

Ответ: , .

Задача 2. Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.

Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.

Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД

Ответ: .

Задача 3. КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной температур газа в цикле.

Тепловые двигатели. Термодинамические циклы. Цикл Карно

Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.

Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.

Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений ( Δ U = 0 ) :

Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3 . 11 . 1 в виде диаграммы ( p , V ) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A 1 , эквивалентную площади под кривой a b c . При сжатии газ совершает отрицательную работу A 2 , равную по модулю площади под кривой c d a . Полная работа за цикл A = A 1 + A 2 на диаграмме ( p , V ) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.

Рисунок 3 . 11 . 1 . Круговой процесс на диаграмме ( p , V ) . a b c – кривая расширения, c d a – кривая сжатия. Работа A в круговом процессе равна площади фигуры a b c d .

Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.

Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.

Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q 1 > 0 и теряет, отдавая холодильнику, количество теплоты Q 2 < 0 . Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:

Q = Q 1 + Q 2 = Q 1 - Q 2 .

Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется Δ U = 0 . Основываясь на первом законе термодинамики, запишем:

Из этого следует:

Работа A , которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q .

Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q 1 , то есть:

η = A Q 1 = Q 1 - Q 2 Q 1 .

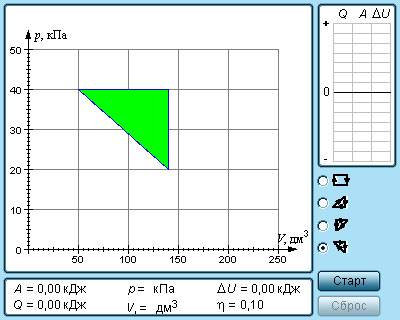
Рисунок 3 . 11 . 2 . Модель термодинамических циклов.

Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть ( 1 – η ) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η < 1 . На рисунке 3 . 11 . 3 проиллюстрирована энергетическая схема тепловой машины.

Рисунок 3 . 11 . 3 . Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q 1 > 0 , A > 0 , Q 2 < 0 ; T 1 > T 2 .

Виды тепловых двигателей

В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3 . 11 . 3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры ( 1 – 2 , 3 – 4 ) и две адиабаты ( 2 – 3 , 4 – 1 ) , дизельного двигателя -две адиабаты ( 1 – 2 , 3 – 4 ) , одну изобару ( 2 – 3 ) и одну изохору ( 4 – 1 ) . Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 % , у дизельного двигателя – приблизительно 40 % .

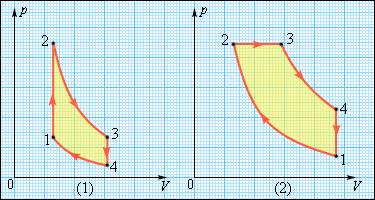
Рисунок 3 . 11 . 4 . Циклы карбюраторного двигателя внутреннего сгорания ( 1 ) и дизельного двигателя ( 2 ) .

Цикл Карно

Круговой процесс, изображенный на рисунке 3 . 11 . 5 , состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

Рисунок 3 . 11 . 5 . Цикл Карно.

Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы ( 1 – 2 ) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T 1 . Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A 12 количество теплоты Q 1 = A 12 . После этого на участке адиабаты ( 2 – 3 ) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A 23 > 0 . Его температура при адиабатическом расширении снижается до величины T 2 . На идущем следующим участке изотермы ( 3 – 4 ) газ приводится в тепловой контакт с холодильником в условиях температуры T 2 < T 1 . Производится процесс изотермического сжатия. Газом совершается некоторая работа A 34 < 0 и отдается тепло Q 2 < 0 , эквивалентное произведенной им работе A 34 . Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T 1 , также совершается работа A 41 < 0 . совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:

A = A 12 + A 23 + A 34 + A 41 .

На диаграмме ( p , V ) данная работа равняется площади цикла.

Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1 – 2 и 3 – 4 , относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.

Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения Δ U его внутренней энергии. Для 1 моля газа верно следующее выражение:

A = - ∆ U = - C V ( T 2 - T 1 ) ,

в котором T 1 и T 2 представляют собой начальную и конечную температуры рабочего тела.

Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:

Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:

η = A Q 1 = A 12 + A 34 Q 12 = Q 1 - Q 2 Q 1 = 1 - Q 2 Q 1 .

С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T 2 и нагревателя T 1 :

η = T 1 - T 2 T 1 = 1 - T 2 T 1 .

Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:

η К а р н о = η m a x

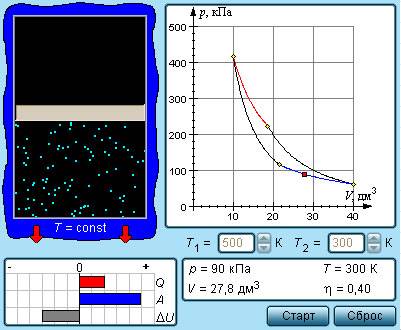
Рисунок 3 . 11 . 6 . Модель цикла Карно.

Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.

Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.

В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме ( p , V ) обходятся против часовой стрелки. На рисунке 3 . 11 . 7 проиллюстрирована энергетическая схема холодильной машины.

Рисунок 3 . 11 . 7 . Энергетическая схема холодильной машины. Q 1 < 0 , A > 0 , Q 2 > 0 , T 1 > T 2 .

Работающее по холодильному циклу устройство может обладать двояким предназначением.

Если полезным эффектом является отбор некоторого количества тепла Q 2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.

Эффективность работы холодильника может быть охарактеризована следующим отношением:

Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 д ж о у л ь затраченной работы. В условиях подобного определения β х может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:

β x = T 2 T 1 - T 2 .

В случае, когда полезным эффектом является передача некоего количества тепла
| Q 1 | нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.

Эффективность β Т теплового насоса может быть определена с помощью отношения:

То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 д ж о у л ь затраченной работы. Из первого закона термодинамики следует:

Следовательно, β Т всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:

§ 59. Тепловые двигатели и холодильные машины. Цикл Карно и его к. П. Д. Для идеального газа

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты,— невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей) .

Принцип действия теплового двигателя приведен на рис. 85. От термостата с более высокой температурой Т₁, называемого нагревателем, за цикл отнимается количество теплоты Q₁, а термостату с более низкой температурой T₂, называемому холодильником, за цикл передается количество теплоты Q₂, при этом совершается работа A = Q₁-Q₂.

Чтобы термический коэффициент полезного действия теплового двигателя (56.2) был =1, должно быть выполнено условие Q₂=0, т. е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Так, французский физик и инженер Н. Л. С. Карно (1796—1832) показал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.

Двигатель второго рода, будь он возможен, был бы практически вечным. Охлаждение, например, воды океанов на 1° дало бы огромную энергию. Масса воды в мировом океане составляет примерно 10 18 т, при охлаждении которой на 1° выделилось бы примерно 10 24 Дж теплоты, что эквивалентно полному сжиганию 10 14 т угля. Железнодорожный состав, нагруженный этим количеством угля, растянулся бы на расстояние 10 10 км, что приблизительно совпадает с размерами Солнечной системы!

Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на рис. 86. Системой за цикл от термостата с более низкой температурой T₂ отнимается количество теплоты Q₂ и отдается термостату с более высокой температурой Т₁ количество теплоты Q₁. Для кругового процесса, согласно (56.1), Q=A, но, по условию, Q=Q₂-Q₁<0, поэтому A<0 и Q₂-Q₁=-A, или Q₁=Q₂+A, т. е. количество теплоты Q₁, отданное системой источнику теплоты при более высокой температуре Т₁, больше количества теплоты Q₂, полученного от источника теплоты при более низкой температуре Т₂, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.

Однако второе начало термодинамики не следует представлять так, что оно совсем запрещает переход теплоты от менее нагретого тела к более нагретому. Ведь именно такой переход осуществляется в холодильной машине. Но при этом надо помнить, что внешние силы совершают работу над системой, т. е. этот переход не является единственным результатом процесса.

Основываясь на втором начале термодинамики, Карно вывел теорему, носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T₁) и холодильников (Т₂), наибольшим к. п. д. обладают обратимые машины; при этом

к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (T₁) и холодильников (T₂), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами).

Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат, и называемый циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

Цикл Карно изображен на рис. 87, где изотермические расширение и сжатие заданы соответственно кривыми 1—2 и 3—4, а адиабатические расширение и сжатие — кривыми 2—3 и 4—1. При изотермическом процессе U=const, поэтому, согласно (54.4), количество теплоты Q₁, полученное газом от нагревателя, равно работе расширения A₁₂, совершаемой газом при переходе из состояния 1 в состояние 2:

При адиабатическом расширении 2—3 теплообмен с окружающей средой отсутствует и работа расширения А₂₃ совершается за счет изменения внутренней энергии (см. (55.1) и (55.8)):

Количество теплоты Q₂, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия А₃₄.

Работа адиабатического сжатия

Работа, совершаемая в результате кругового процесса,

и, как можно показать, определяется площадью, выполненной в цвете на рис. 87.

Термический к. п. д. цикла Карно, согласно (56.2),

Применив уравнение (55.5) для адиабат 2—3 и 4—1, получим

Подставляя (59.1) и (59.2) в формулу (56.2) и учитывая (59.3), получим

т. е. для цикла Карно к. п. д. действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при T₁=400 К и T₂ = 300К =0,25, Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то =0,5. К. п. д. всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.

Обратный цикл Карно лежит в основе действия тепловых насосов. В отличие от холодильных машин тепловые насосы до-

лжны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Часть этой энергии отбирается от окружающей среды с более низкой температурой, а часть — получается за счет механической работы, производимой, например, компрессором.

Теорема Карно послужила основанием для установления термодинамической шкалы температур. Сравнив левую и правую части формулы (59.4), получим

т. е. для сравнения температур T₁ и T₂ двух тел необходимо осуществить обратимый цикл Карно, в котором одно тело

используется в качестве нагревателя, другое — холодильника. Из равенства (59.5) видно, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному. Согласно теореме Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то определенного термометрического тела. Отметим, что практически таким образом сравнивать температуры трудно, так как реальные термодинамические процессы, как уже указывалось, являются необратимыми.

Контрольные вопросы

• В чем суть закона Больцмана о равнораспределении энергии по степеням свободы молекул? Почему колебательная степень свободы обладает вдвое большей энергией, чем поступательная и вращательная?

• Что такое внутренняя энергия идеального газа? Какими параметрами она определяется? В результате каких процессов может изменяться внутренняя энергия системы? Что такое теплоемкость газа? Какая из теплоемкостей — C_v или С_р — больше и почему? Как объяснить температурную зависимость молярной теплоемкости водорода? Чему равна работа изобарного расширения моля идеального газа при нагревании на 1 К? Нагревается или охлаждается идеальный газ, если он расширяется при постоянном давлении? Температура газа в цилиндре постоянна. Запишите на основе первого начала термодинамики соотношение между сообщенным количеством теплоты и совершенной работой.

• Газ переходит из одного и того же начального состояния 1 в одно и то же конечное состояние 2 в результате следующих процессов: а) изотермического; б) изобарного; в) изохорного. Рассмотрев эти процессы графически, показать: 1) когда работа расширения максимальна; 2) когда газу сообщается максимальное количество теплоты.

• Газ переходит из одного и того же начального состояния 1 в одно и то же конечное состояние 2 в результате следующих процессов: а) изобарного процесса; б) последовательных изохорного и изотермического процессов. Рассмотрите эти переходы графически. Одинаковы или различны в обоих случаях: 1) изменение внутренней энергии? 2) затраченное количество теплоты?

• Почему адиабата более крута, чем изотерма?

• Как изменится температура газа при его адиабатическом сжатии?

• Показатель политропы n>1. Нагревается или охлаждается идеальный газ при сжатии?

• Чем отличаются обратимые и необратимые процессы? Почему все реальные процессы необратимы?

• В каком направлении может изменяться энтропия замкнутой системы? незамкнутой системы?

• Дайте понятие энтропии (определение, размерность и математическое выражение энтропии для различных процессов).

• Изобразите в системе координат Т, S изотермический и адиабатический процессы.

• Возможен ли процесс, при котором теплота, взятая от нагревателя, полностью преобразуется в работу?

• Представив цикл Карно на диаграмме р, V графически, укажите, какой площадью определяется: 1) работа, совершенная над газом; 2) работа, совершенная самим расширяющимся газом.

• Представьте графически цикл Карно в переменных Т, S.

9.1. Азот массой 1 кг находится при температуре 280 К. Определить: 1) внутреннюю энергию молекул азота; 2) среднюю кинетическую энергию вращательного движения молекул азота. Газ считать идеальным. [1) 208 кДж; 2) 83,1 кДж ]

9.2. Определить удельные теплоемкости c_v и с_р некоторого двухатомного газа, если плотность этого газа при нормальных условиях 1,43 кг/м 3 . [ с_v = 650 Дж/(кг*К), с_р = 910 Дж/(кг*К)]

9.3. Водород массой m = 20 г был нагрет на T=100 К при постоянном давлении. Определить: 1) количество теплоты Q, переданное газу; 2) приращение U внутренней энергии газа; 3) работу А расширения. [1) 29,3 кДж; 2) 20,9 кДж; 3) 8,4 кДж ]

9.4. Кислород объемом 2 л находится под давлением 1 МПа. Определить, какое количество теплоты необходимо сообщить газу, чтобы увеличить его давление вдвое в результате изохорного процесса. [ 5 кДж ]

9.5. Некоторый газ массой 2 кг находится при температуре 300 К и под давлением 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в три раза. Работа, затраченная на сжатие, А= -1,37 кДж. Определить: 1) какой это газ; 2) первоначальный удельный объем газа. [1) гелий; 2) 1,25 м 3 /кг ]

9.6. Двухатомный идеальный газ занимает объем V₁ = 1 л и находится под давлением р₁ = = 0,1 МПа. После адиабатического сжатия газ характеризуется объемом V₂ и давлением р₂. В результате последующего изохорного процесса газ охлаждается до первоначальной температуры, а его давление р₃=0,2 МПа. Определить: 1) объем V₂; 2) давление р₂. Представить эти процессы графически. [ 1) 0,5 л; 2) 0,26 МПа ]

9.7. Идеальный газ количеством вещества v = 2 моль сначала изобарно нагрели так, что его объем увеличился в n=2 раза, а затем изохорно охладили так, что давление газа уменьшилось в n=2 раза. Определить приращение энтропии в ходе указанных процессов. [ 11,5 Дж/К ]

9.8. Тепловая машина, совершая обратимый цикл Карно, за один цикл совершает работу 1 кДж. Температура нагревателя 400 К, а холодильника 300 К. Определить: 1) к.п.д. машины; 2) количество теплоты, получаемое машиной от нагревателя за цикл; 3) количество теплоты, отданное холодильнику за цикл. [ 1) 25%; 2) 4 кДж; 3) 3 кДж ]

9.9. Идеальный газ совершает цикл Карно, термический к.п.д. которого равен 0,3. Определить работу изотермического сжатия газа, если работа изотермического расширения составляет 300 Дж. [-210 Дж]

*Термодинамическая система, которая может обмениваться теплотой с телами без изменения температуры

* В. Ф. Г. Нернст (1864—1941) — немецкий физик и физикохимик.

Читайте также: